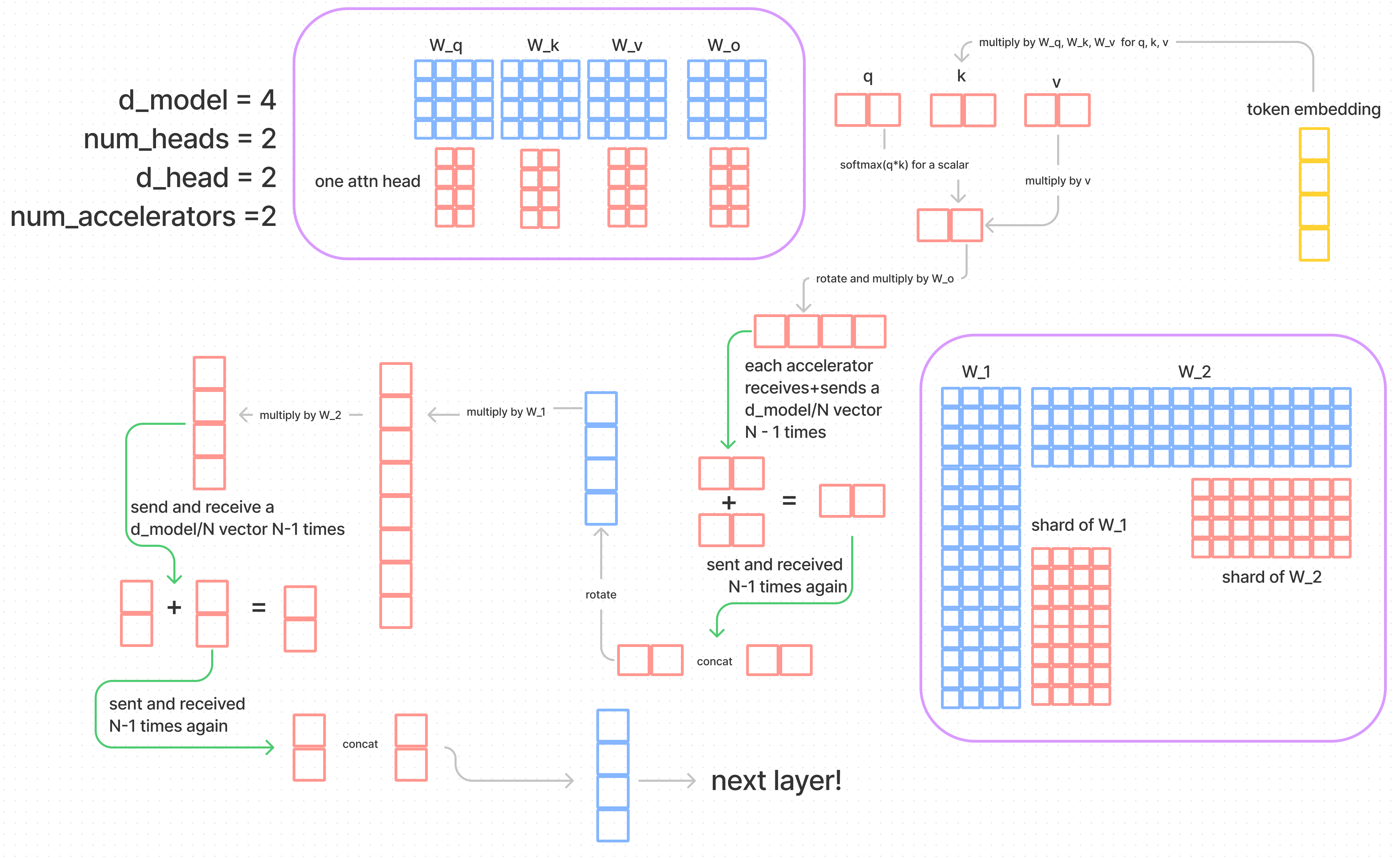
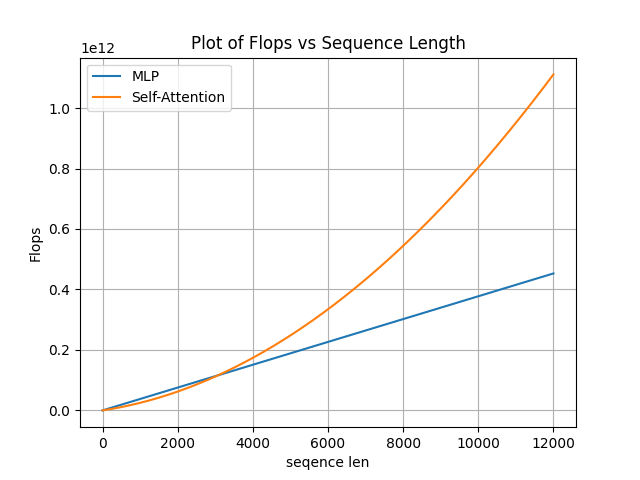
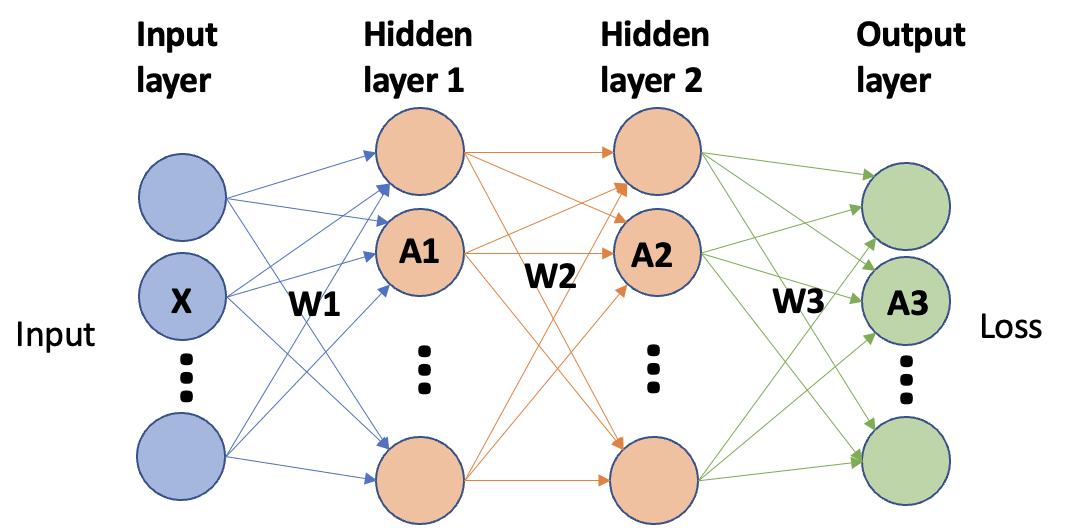
前言

随着Sora和kimi的大火, 视频模型和超长序列语言模型的实践不断被人们摆到更重要的位置, 这篇博客主要从需求和基本思路以及实践这几个方面来讲解一下序列并行相关的内容。

需求

从产品需求的角度看, 长序列是必然的需求。从语言模型看, 做超长文本检索以及摘要有确定的需求(例如平时看文献)。sora能够生成超长视频, 在使用vanilla attention的情况下, attention的序列长度将为(T, H, W), 也就是时长, 高度, 宽度三者的乘积增长, 序列长度比图像模型上一个量级, 这也一定会成为sora训练和推理的难题。尽管当前的flash attention的显存消耗能够被优化到线性增长的程度, 但是当序列长度足够长, 显存依然可能不够。

就此,

• 我们的问题被定义为: 如何让transformer支持超长序列的训练和推理
• 问题的核心: 来源于显存装不下超长序列带来的显存需求, 而非模型太大带来的显存溢出
• 可能方法: 优化显存或者使用多GPU并行计算分摊显存和计算

基本思路

首先我们需要将一句话铭记于心, 默念三遍:

transformer模型中, 序列的概念仅在attention这个操作中被需要, 在做MLP等其他操作时, 打乱序列甚至打乱batch都是可以的, 只要在attention操作时将序列顺序恢复即可。

对于超长序列支持问题, 可能最直接的想法就是使用张量并行, 将模型切分, 对应的序列也在(B, L, D)的D维度被切分, 从而可以节省显存。

但是需要注意的是, 我们遇到的问题是来自于序列过长, 而模型并非过大, 特别是diffusion的模型都还非常小, 一张显卡放的下。其次, 使用模型并行中途计算需要的通信同步开销较大, 小模型做张量并行不值得。

再次回想我们铭记于心的话, 我们可以思考, 可否将序列(B, L, D) 在L维度切分, 在多张卡上做MLP等和序列无关的操作(无需通信), 在做attention时将相关的内容从其他GPU获取, 再进行attention操作, 再将计算结果同步到其他GPU上。这样比张量并行的好处在于无需切分模型, 减少通信量, 提高模型的吞吐与性能。

基本实现

接下来介绍几个实现了序列并行的库或者算法:

约定

• B: batch size
• L: seq len
• D: hidden dim
• A: attention head size
• Z: number of attention heads
• N: number of GPU
• Z x A = D

N个GPU上存储了(B, L/N, D)的序列, 给出在分布式情况下计算self attention的算法。

Ring self attention(RSA)

这样的方式是通过在query的L维度上切分进行分布式的attention的计算。通信的方式是通过进程之间换装传递K和V的分块然后得到最后的计算结果, 这样的算法不受到Z大小的限制, 对GPU的数量是可扩展的。

第一阶段-环状传递分块的K来得到attention map

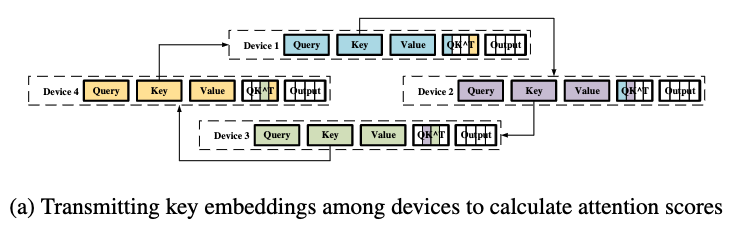
第二阶段-环状传递分块的V得到最后的结果

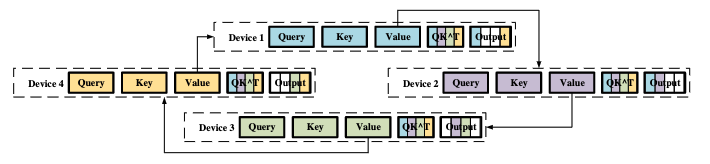
通俗的理解ring attention的机制, 其核心的并行的点在于, attention的计算是可以在query的sequence lens的维度上分块的, 也就是一部分的query和完整的key和value就可以得出此部分qeury对应的计算结果。而由于序列过长, key和value也被打散在不同进程中, 所以需要从其他进程不断传递并计算从而得到完整的key和value以得到最终结果。

不断集齐key和value这样的过程, 最简单的方式就是通过进程顺序点到点的方式完成, 显然这样的效率是不够高的, 在传递过程中如何尽量把各个节点之间的带宽利用好, 同时做好计算和通信的重叠, 而ring的方式就是系统领域典型的算法和方式, 能够做到较好的利用带宽, 在有良好的实线的情况下, 可以做到计算和通信的重叠。

Deepspeed ulyss

Attention的另外一种并行方式就是类似于张量并行的按照Attention head进行切分。也就是每个进程拥有完整的序列长度, 但是只有一部分的head个数, 这样同样能够节省显存, 而且这样的方法可以做到不改变Attention的实现, 也就是任何的attention算法都和Deepspeed ulyss兼容。但是缺点是并行的卡的数量不超过头的个数Z。

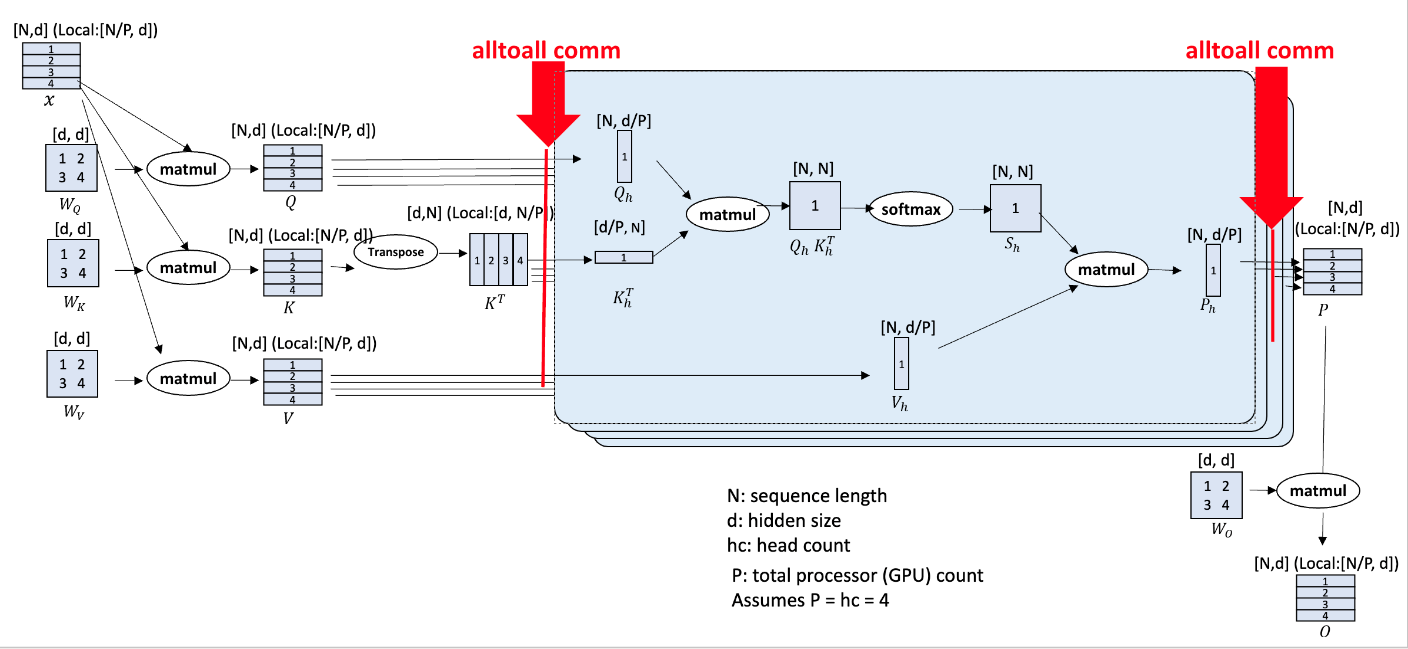
序列并行要求在MLP层无额外的操作, 所以每个进程中应该有部分的序列, 但是包含完整的attention head, 在进行attention并行时, 又要求每个进程需要完整的序列且是部分的头。所以可以遇见的是在进行attention操作前, 通过通信算子使得每个进程拥有(B, L/N, ZxA) 转化到每个进程拥有(B, L, ZxA/N)的序列内容。attention 操作结束后, 再通过通信算子使得每个进程从拥有(B, L, ZxA/N)的序列内容转化为(B, L/N, ZXA)的序列内容。课件仅需要操作开始前, 结束后需要进行通信, attention的算子是完全独立的, 所以可以采用任意attention算子的实现。

Deepspeed ulyss的实现也非常简洁, 通过源代码就可以看到:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102

# https://github.com/microsoft/DeepSpeed/blob/master/deepspeed/sequence/layer.py
import torch

from typing import Any, Tuple
from torch import Tensor
from torch.nn import Module

import deepspeed.comm as dist

def single_all_to_all(input, scatter_idx, gather_idx, group):
    seq_world_size = dist.get_world_size(group)
    inp_shape = list(input.shape)
    inp_shape[scatter_idx] = inp_shape[scatter_idx] // seq_world_size
    if scatter_idx < 2:
        input_t = input.reshape(
            [seq_world_size, inp_shape[scatter_idx]] + \
            inp_shape[scatter_idx + 1:]
        ).contiguous()
    else:
        # transpose groups of heads with the seq-len parallel dimension, so that we can scatter them!
        input_t = input.reshape(
            [-1, seq_world_size, inp_shape[scatter_idx]] + \
            inp_shape[scatter_idx + 1:]
        ).transpose(0, 1).contiguous()

    output = torch.empty_like(input_t)
    dist.all_to_all_single(output, input_t, group=group)

    # if scattering the seq-dim, transpose the heads back to the original dimension
    if scatter_idx < 2:
        output = output.transpose(0, 1).contiguous()

    return output.reshape(
        inp_shape[: gather_idx] + \
        [inp_shape[gather_idx] * seq_world_size,] + \
        inp_shape[gather_idx + 1:]).contiguous()

class _SeqAllToAll(torch.autograd.Function):

    @staticmethod
    def forward(ctx: Any, group: dist.ProcessGroup, input: Tensor, scatter_idx: int, gather_idx: int) -> Tensor:

        ctx.group = group
        ctx.scatter_idx = scatter_idx
        ctx.gather_idx = gather_idx

        return single_all_to_all(input, scatter_idx, gather_idx, group)

    @staticmethod
    def backward(ctx: Any, *grad_output: Tensor) -> Tuple[None, Tensor, None, None]:
        return (None, _SeqAllToAll.apply(ctx.group, *grad_output, ctx.gather_idx, ctx.scatter_idx), None, None)

class DistributedAttention(torch.nn.Module):
    """Initialization.

    Arguments:
        local_attention (Module): local attention with q,k,v
        sequence_process_group (ProcessGroup): sequence parallel process group
        scatter_idx (int): scatter_idx for all2all comm
        gather_idx (int): gather_idx for all2all comm
    """

    def __init__(
        self,
        local_attention: Module,
        sequence_process_group: dist.ProcessGroup,
        scatter_idx: int = 2,
        gather_idx: int = 0,
    ) -> None:

        super(DistributedAttention, self).__init__()
        self.local_attn = local_attention
        self.spg = sequence_process_group
        self.scatter_idx = scatter_idx
        self.gather_idx = gather_idx

    def forward(self, query: Tensor, key: Tensor, value: Tensor, *args: Any) -> Tensor:
        """ forward

        Arguments:
            query (Tensor): query input to the layer
            key (Tensor): key input to the layer
            value (Tensor): value input to the layer
            args: other args

        Returns:
            * output (Tensor): context output
        """
        # TODO Merge three alltoall calls into one
        # TODO (Reza): change the api on the megatron-deepspeed side so that we only receive all data (q,k, and v) together!
        #in shape : e.g.,  [s/p:h:]
        query_layer = _SeqAllToAll.apply(self.spg, query, self.scatter_idx, self.gather_idx)
        key_layer = _SeqAllToAll.apply(self.spg, key, self.scatter_idx, self.gather_idx)
        value_layer = _SeqAllToAll.apply(self.spg, value, self.scatter_idx, self.gather_idx)

        #out shape : e.g., [s:h/p:]
        context_layer = self.local_attn(query_layer, key_layer, value_layer, *args)

        output = _SeqAllToAll.apply(self.spg, context_layer, self.gather_idx, self.scatter_idx)

        #out e.g., [s/p::h]
        return output

核心实现就是_SeqAllToAll这个函数的实现, 给定group, 在forward的时候通过通信将当前进程需要的序列聚积到当前进程, 在backward时, 我们通过后层收到的梯度也应该通过通信分发到正确的进程中, 并从别的进程中取到属于自己进程内容的梯度。以q, k, v的通信算子举例:

• forward时, 进程拥有(B, L/N, ZxA) 的序列内容, 通信后进程拥有(B, L, ZxA/N)
• backward时, 进程收到的梯度是(B, L, ZxA/N)内容的梯度, 但是本进程需要正确回传的梯度是(B, L/N, ZxA) 序列的梯度, 所以通过同样的算法得到正确的梯度

对于通信的算子, 最简单的算子就是AlltoAll, 使得每个进程在某个瞬间拥有(B, L, ZxA)的序列, 然后丢弃不需要的部分进行计算, 显然这样的方式会出现不必要的显存分配, 没有做到足够优雅的节省显存问题, 所以deepspeed使用的事AlltoAll_single这样的通信算子, 可以理解为将张量内容在进程间的某两个维度进行转置, 通信过程无需分配很多内容, 进一步提高效率。为了大家对AlltoAll_single有更好的理解, 这里附上pytorch对应算子的文档:

torch.distributed.all_to_all_single(output, input, output_split_sizes=None, input_split_sizes=None, group=None, async_op=False)

1
2
3
4
5
6
7
8
9
10
11
12
13

>>> input = torch.arange(4) + rank * 4
>>> input
tensor([0, 1, 2, 3])     # Rank 0
tensor([4, 5, 6, 7])     # Rank 1
tensor([8, 9, 10, 11])   # Rank 2
tensor([12, 13, 14, 15]) # Rank 3
>>> output = torch.empty([4], dtype=torch.int64)
>>> dist.all_to_all_single(output, input)
>>> output
tensor([0, 4, 8, 12])    # Rank 0
tensor([1, 5, 9, 13])    # Rank 1
tensor([2, 6, 10, 14])   # Rank 2
tensor([3, 7, 11, 15])   # Rank 3

总结

本文介绍了序列并行解决的问题, 以及两种主流的实现序列并行的方式。其实两种序列并行可以混合使用, 从而达到更好的并行度和性能。同时在语言模型中, 带causal mask的情况下, 简单的序列切分会导致进程间计算负载不均衡, 随后衍生出striped attention。

transformer 性能分析

简介

随着模型的不断变大, 模型的推理和训练成本在不断的提高, 如何更好的优化模型训练和推理的性能成为非常重要的领域, 10%的性能提升可能带来数十万乃至数百万成本的节省。

主要的性能优化一般来自于在计算逻辑不变的情况下对硬件更好的优化和利用, 或者在少量损失模型计算精度的情况下减少模型推理的计算量和放存量, 从而提高性能。

这篇博客主要学习这篇博客的分析思路, 先从内容的翻译和理解入手, 随后将博客的内容扩展到diffusion transformer以及训练相关的性能分析, 从而给如何优化以更好的理论指导。

约定和基础

在本博客中我们对数值的约定和参考的博客有一定的出入, 对于内存占用, 我们只计算元素的个数, 也就是不考虑每个参数的位宽, 只计算参数的个数。默认情况下

矩阵向量乘的计算量:

对于矩阵向量乘 , 的计算量为: 。对于 ,矩阵矩阵乘的计算量为 , 其中系数2分别为乘和加。

kv cache解读

transformer在推理时分两个阶段,

1. 是处理给定的prompt(是一次简单的forward, token一起喂入模型中)
2. 随后是不断自回归地产生后续的token序列(每次只产生一个token)。这里需要提一点的是, transformer解码时之前所有计算的token对应的latent都和后续的token没有关系(因为attention mask的存在, 这也是为什么模型是autoregressive, 详情请见)。

因为之前的token和后面的token无关系, 所以这部分的值无需重复计算, 但是历史的K和V在每次计算中都需要(只被self attention 需要), 所以需要将每个transformer block的历史KV保存起来, 这部分保存的内容被称之为KV cache, 在使用KV cache的情况下, transformer每次只需要输入一个token用以计算, 无需输入再次前面的全部序列, 计算量是随着token个数线性增长。

对于每个token, 需要保存的KV cache参数量为:

其中(1+1)表示k和v。

对于计算一个新的token的KV cache, 我们需要的计算量为:

同时我们需要的访存量为:

总体而言, 是取参数的放存量占大头, token的访存量可忽略。

对于A100GPU而言, fp16的性能为312TFlops, 内存带宽为1.5T/s, 则用于计算一个token的KV访存耗时和计算耗时为:

可见, 用于访存的时间是用于计算的208倍之多, 这说明transformer解码的过程是内存瓶颈, 内存带宽。造成这种瓶颈的主要原因是解码时只计算一个token, 计算量小, 而模型的参数很大。

需要注意的是, KVcache的存在并不是仅仅为了节省计算KV本身所需要的计算量, 而是节省了前面所有token通过模型所需要的计算量。如果没有KVcache, transformer的解码过程会为平方级增长的计算量(第一次forward1个token, 第二次forward2个token, 第三次forward3token….), 这将难以承受。

💡 如果我们增大batch size, 能够获得在每次解码时更多的计算量和相近的访存量(因为主要放存量在模型权重), 而由于计算非常便宜, 我们的收益是大的(额外花1%的时间, 多获得一个token的解码), 这可能会提高每个token的延迟, 但是能够极大增加模型token的吞吐。对此已经有研究(ORCA)进行了优化, 使得模型吞吐上了一个量级, 造福了人类。

容量计算

接下来进行简单的容量计算分析, 对于一个52B(52e9 numel)的模型, 如果采用半精度存储, 则大约需要104GB(104e9 Bytes, two bytes for each parameter)的空间, 单卡无法放下, 同时在推理时KVcache 也需要占用空间。

给定4卡的A100 40G卡, 我们可以简单计算可以sample 的token数量。已知模型已经占了104G, 只有16G留给了KVcache。每个token需要的空间为: 所以16G大约可以容下8000token。

模型并行

我们一般讨论的模型并行是指张量并行, 也就是将模型纵向切开, 每张卡上都有所有block参数的一部分。模型并行能够使得每张卡只承受一部分的模型参数存储和有一部分的计算量, 这些部分收到卡的数量的影响。模型并行会额外带来的开销是分块计算后同步计算结果的通信开销, 这部分会影响到推理的延迟。

此外, 将模型横向切分, 每张卡包含了若干个完整的block, 这样的方法被称为流水线并行, 由于每个token会依次通过所有block也就会依次通过每张卡一次, 每次只有一张GPU在进行计算, 所以每个token的延迟和单卡基本一致, 但是通过流水线的方法不断喂入token, 总的吞吐可以达到和4张卡一致。流水线并行唯一的好处在于需要的通信量比较小, 这适合卡间带宽比较小的场景。流水线并行需要在每张卡之间传递latent, 而张量并行需要每个block之间进行每张卡之间的通信, 通信量上一个量级。

矩阵向量乘分块并行

考虑权重矩阵, GPU数量为N, 输入向量大小。则输出大小应当为。

分块后, 每个GPU的权重矩阵大小为, 输入同时也被切分被向量大小 。每个GPU分别分配到的矩阵向量乘, 得到的输出大小为。每个得到的此时我们可以知道虽然每个GPU得到的结果和输出大小一致, 但是可知真正的结果是每个GPU计算得到的结果做求和得到的, 这就需要做一次All reduce的操作, 是的每个GPU上都是正确的结果之后, 再进行切分, 进行后续的分块并行计算。

attention的并行

Attention的并行是通过在attention head的层面进行并行。head的切分维度刚好是在 中的n, 所以之前的计算结束后, 无需额外的通信就可以直接进行attention计算(前提是num head是卡数的n倍)。计算结束后, 甚至可以通过之后再进行通讯合并。同理, KVcache也是在head这个维度上存储在不同的GPU上。

各个模块计算量和访存量分析

标记:在diffusion transformer中, num_tokens = s = T * H * W

MLP

• mlp的参数为 in_d , mid_d, out_d 。通常情况而言, in_d = out_d, mid_d = 4 * in_d

• Flops =

• 访存量:

  这里的访存量包括把结果写到内存中。

Vanilla self attention

• attention参数为: in_d, mid_d , out_d 。通常情况而言, 三者相等。
• Flops =
• 访存量:

Vanilla cross attention

• 参数为: in_d, context_d, mid_d, out_d, 通常只有context_d 和其他三者不同
• Flops =
• 访存量:

Spatial self attention

• attention参数为: in_d, mid_d , out_d 。通常情况而言, 三者相等。
• Flops =
• 访存量:

Spatial cross attention

• 参数为: in_d, context_d, mid_d, out_d, 通常只有context_d 和其他三者不同

• Flops =

• 访存量:

  计算量和vanilla一致

temprol self attention

• attention参数为: in_d, mid_d , out_d 。通常情况而言, 三者相等。
• Flops =
• 访存量:

小讨论

可知MLP的计算量随着序列长度线性增长, 而sefl-Attention的计算量是平方级增长, 在这里我们可以计算一下经典场景下, 当序列长度到达什么水平时, Attention的计算量会成为主要部分。

in_d = mid_d = out_d, MLP mid_d=4in_d

则MLP的计算量公式为:

Attention计算量公式为:

在dim = 1536的情况下计算, 画图如下:

在大约3K以后, Attention的计算成为主要部分。

backward分析

考虑以下的三层MLP, x为输入, 为三个权重矩阵, 为三个激活, 最后和ground truth计算得到loss。

remark:

注意到, 因为input x 无需计算梯度, 所以对于第一层而言, backward节省了约一半的计算量。所以在网络较深的情况下, backward的计算时间约为forward计算时间的两倍。

参考资料

• https://kipp.ly/transformer-inference-arithmetic/
• https://www.alignmentforum.org/posts/fnjKpBoWJXcSDwhZk/what-s-the-backward-forward-flop-ratio-for-neural-networks